2019-10-16 •

On the back-propagation of CG linear system solvers

We have seen from the previous article that the dominant eigen-decomposition as a function primitive for AD needs CG or other linear system solver for its backward pass. In this article, we will furthermore investigate the feasibility of carrying out back-propagation of this CG process itself, since this can be encountered in some practical situations.

$\renewcommand{\vec}[1]{\mathbf{#1}}$

$\renewcommand{\ud}{\mathrm{d}}$

Background

Recall that in the settings of dominant eigen-decomposition process, one certain eigenvalue $\alpha$ and corresponding eigenvector $\vec{x}$ are returned for a $N$-dimensional real symmetric matrix $A$. In real applications, if the adjoint $\overline{\vec{x}}$ of the eigenvector is not zero, then the backward pass is somewhat nontrivial, which involves solving a linear system of the following form:

$(A - \alpha I)\boldsymbol{\lambda}_0 = (1 - \vec{x}\vec{x}^T) \overline{\vec{x}}, \quad \vec{x}^T \boldsymbol{\lambda}_0 = 0. \label{eq: dominant eigen-decomposition AD}$

Under the assumption that the eigenvalue $\alpha$ is non-degenerate, this is a “low-rank” linear system, in the sense that the coefficient matrix $A - \alpha I$ is of rank $N -1$ and thus singular. Nevertheless, the solution for the vector $\boldsymbol{\lambda}_0$ is unique, because the singular matrix $A - \alpha I$, when represented in the $(N - 1)$-dimensional subspace spanned by the $N - 1$ eigenvectors other than $\vec{x}$, is effectively non-singular.

It turns out that for certain practical applications, such as when 2nd derivative of certain quantities of physical interest is needed, we have to work on the back-propagation of the CG process of linear system solver itself to make automatic differentiation possible. We will study this mathematical problem in some details below.

Warm up: Full-rank linear system solver

As a warm-up exercise, we will consider the simple case where the coefficient matrix of the linear system is non-singular, since the result in this case is fairly straight-forward. Specifically, let $A$ be a $N$-dimensional non-singular, real symmetric matrix (which indicates that all of its $N$ eigenvalues are nonzero), and $\vec{b}$ be an arbitrary vector. The (unique) output $\vec{x}$ satisfies the equation $A \vec{x} = \vec{b}$. The computation graph is as follows:

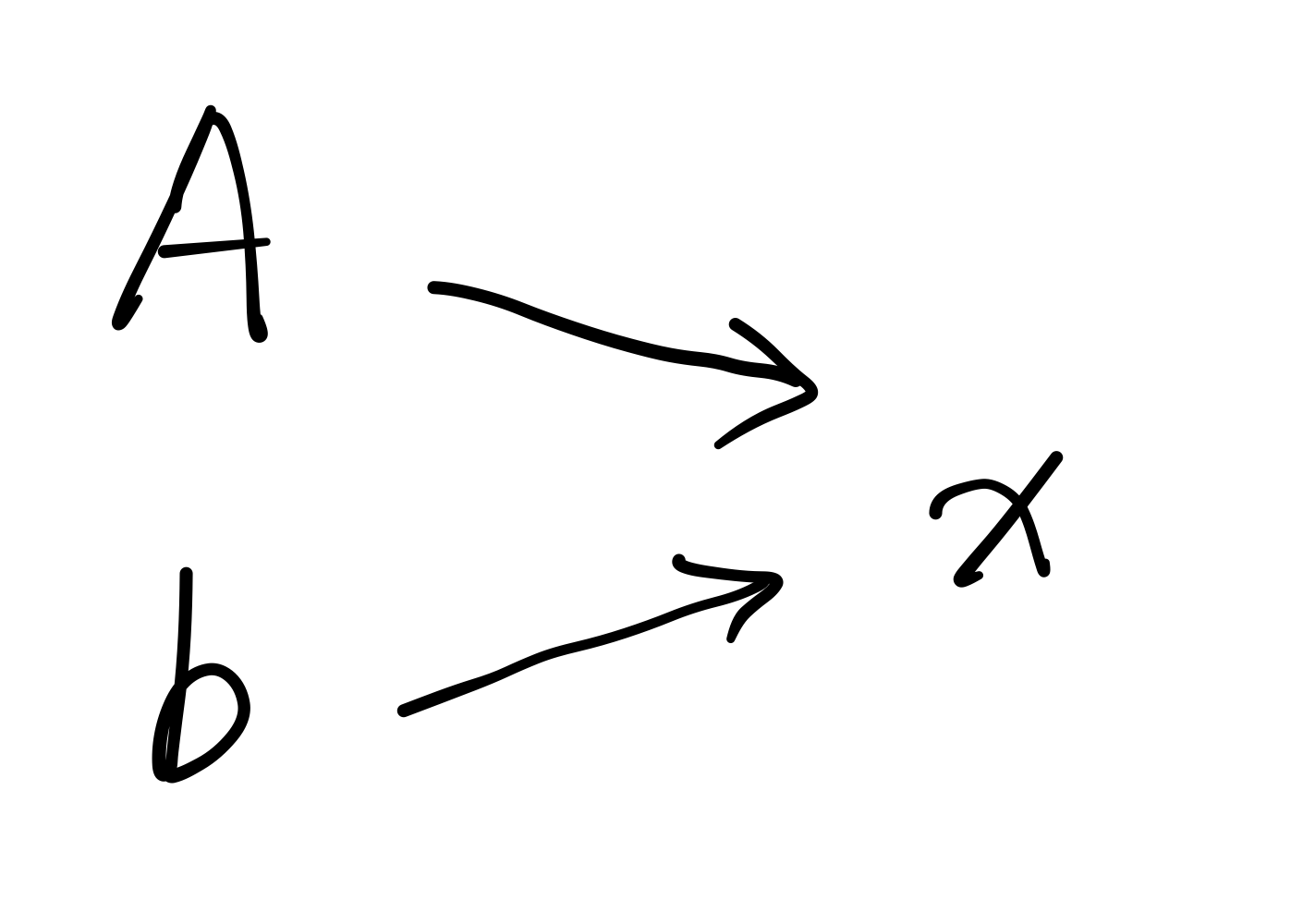
CG_full_rank

To derive the backward formula, we have

$\ud A \vec{x} + A \ud \vec{x} = \ud \vec{b}. \quad \rightarrow \quad \ud \vec{x} = A^{-1}(\ud \vec{b} - \ud A \vec{x}). \label{eq: full rank CG equation1}$

On the other hand, the differential of the loss $\mathcal{L}$ can be expressed as

$\ud \mathcal{L} = \overline{\vec{x}}^T \ud \vec{x} = \mathrm{Tr} \left(\overline{A}^T \ud A\right) + \overline{\vec{b}}^T \ud \vec{b}. \label{eq: full rank CG equation2}$

Combining Eq. $\eqref{eq: full rank CG equation1}$ and $\eqref{eq: full rank CG equation2}$, one immediately obtains

$\overline{\vec{b}} = A^{-1} \overline{\vec{x}}, \quad \overline{A} = - A^{-1} \overline{\vec{x}} \vec{x}^T.$

Or, expressed without the appearance of matrix inverse:

$\textrm{$\overline{\vec{b}}$ satisfies } A \overline{\vec{b}} = \overline{\vec{x}}, \\ \overline{A} = - \overline{\vec{b}} \vec{x}^T. \label{eq: full-rank linear system solver AD}$

This is the final result. One can see that the backward pass of full-rank linear system solver involves solving another full-rank linear system.

Low-rank linear system solver

The formulation in the last section is fairly simple, yet is not as complicated to cover some real situations of interests, such as the backward pass of dominant eigen-decomposition described above. In this section, we will study the low-rank version of linear system solver to some extent.

The settings are as follows. Let $A$ be an $N$-dimensional real symmetric matrix of rank $N - 1$. This indicates that $A$ has $N - 1$ eigenvectors $\alpha_2, \cdots, \alpha_N$ with nonzero eigenvalues $\lambda_2, \cdots, \lambda_N$, respectively, other than a single eigenvector $\alpha$ with eigenvalue zero. Let $\vec{b}$ be an arbitrary vector lying in the $(N - 1)$-dimensional subspace spanned by $\alpha_2, \cdots, \alpha_N$, the goal of the computation process is the unique solution for $\vec{x}$ of the following equations:

$A \vec{x} = \vec{b}, \quad \alpha^T \vec{x} = 0. \label{eq: low-rank linear system problem}$

Rigorously speaking, the information about the eigenvector $\alpha$ of eigenvalue zero is contained in the given matrix $A$. However this information is somewhat hard to extract directly, and in practice one finds it more convenient to treat $\alpha$ as an independent input to the process. All this being said, the computation graph we will work on is slightly different with the full-rank case and shown in the figure below.

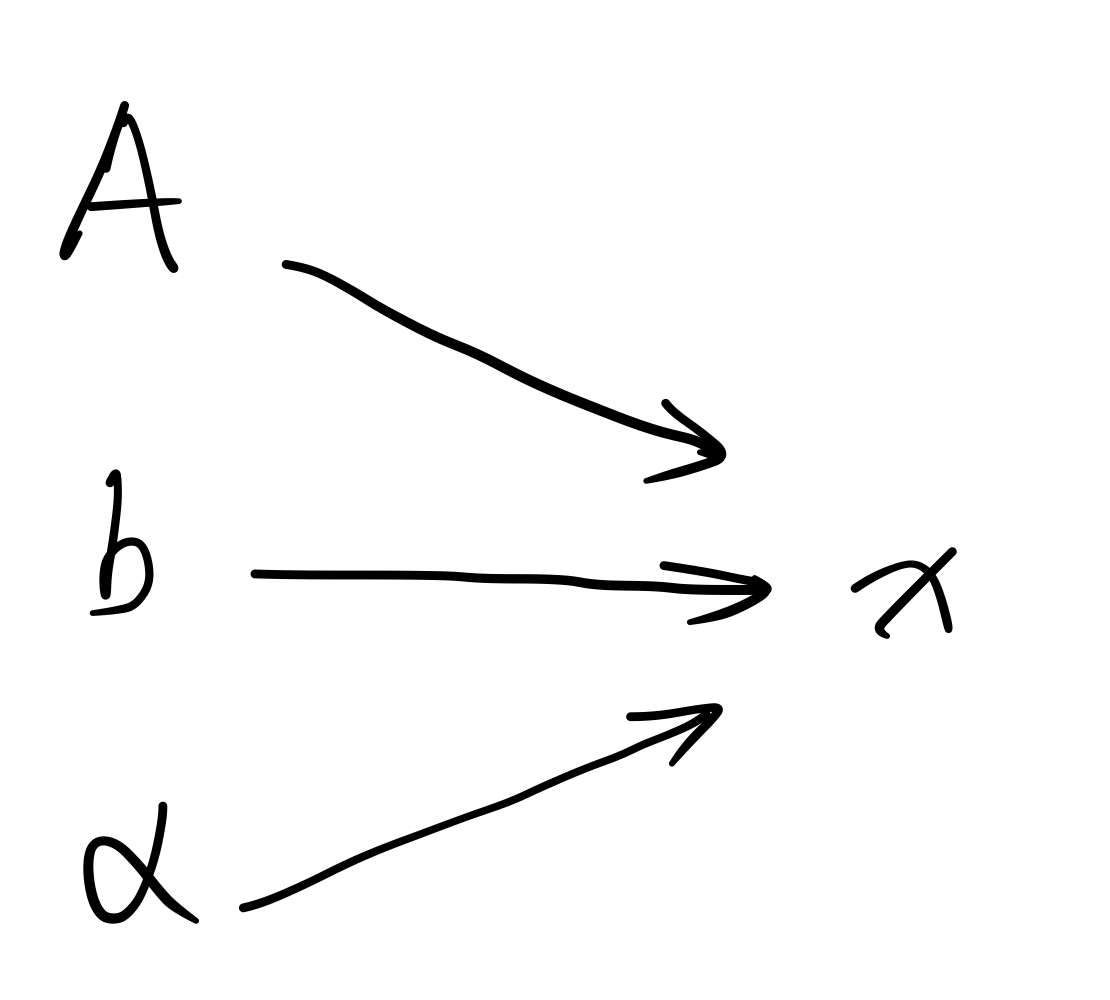
CG_low_rank

To derive the back-propagation of this process, we introduce following notations:

$D \equiv \begin{pmatrix} \lambda_2 \\ & \ddots \\ & & \lambda_N \end{pmatrix}, \quad U \equiv \begin{pmatrix} \vert & & \vert \\ \alpha_2 & \cdots & \alpha_N \\ \vert & & \vert \end{pmatrix}.$

Note that $D$ is non-singular, since all of its diagonal elements are nonzero. It’s not hard to see that they satisfy the following relationships:

$A = U D U^T. \label{eq: A}$ $U^T U = I_{N-1}. \label{eq: orthogonal relation}$ $U U^T = I_N - \alpha \alpha^T. \label{eq: completeness relation}$

where $I_{N-1}$ denotes the $(N-1)$-dimensional identity matrix. From Eq. $\eqref{eq: low-rank linear system problem}$, we have

$A \ud \vec{x} = \ud \vec{b} - \ud A \vec{x}. \label{eq: derivative1}$ $\ud \alpha^T \vec{x} + \alpha^T \ud \vec{x} = 0. \label{eq: derivative2}$

Making use of Eq. $\eqref{eq: completeness relation}$, one could expand the differential $\ud \vec{x}$ in the complete diagonalization basis and get

$\ud \vec{x} = U U^T \ud \vec{x} + \alpha \alpha^T \ud \vec{x}. \label{eq: dx}$

Combining Eq. $\eqref{eq: A}$ and $\eqref{eq: derivative1}$, and making use of Eq. $\eqref{eq: orthogonal relation}$, one can obtain that

$U^T \ud \vec{x} = D^{-1} U^T (\ud \vec{b} - \ud A \vec{x}). \label{eq: UTdx}$

Substituting Eq. $\eqref{eq: UTdx}$ and $\eqref{eq: derivative2}$ into $\eqref{eq: dx}$ thus yields:

$\ud \vec{x} = U D^{-1} U^T (\ud \vec{b} - \ud A \vec{x}) - \alpha \vec{x}^T \ud \alpha.$

Comparing this result with the standard formula

$\ud \mathcal{L} = \overline{\vec{x}}^T \ud \vec{x} = \mathrm{Tr}\left(\overline{A}^T \ud A\right) + \overline{\vec{b}}^T \ud \vec{b} + \overline{\alpha}^T \ud \alpha.$

one can immediately obtain the following result:

$\begin{align} \overline{\vec{b}} &= U D^{-1} U^T \overline{\vec{x}}, \label{eq: first equation} \\ \overline{A} &= - U D^{-1} U^T \overline{\vec{x}} \vec{x}^T, \\ \overline{\alpha} &= - \vec{x} \alpha^T \overline{\vec{x}}. \end{align}$

To eliminate the matrix $D$ and $U$, which contain the unknown information about the full spectrum of $A$, we can multiply both sides of the first equation $\eqref{eq: first equation}$ by $A$ and get

$A \overline{\vec{b}} = (1 - \alpha \alpha^T) \overline{\vec{x}}.$

where we have again used the relations $\eqref{eq: A}$, $\eqref{eq: orthogonal relation}$ and $\eqref{eq: completeness relation}$. The equation above cannot uniquely determine $\overline{\vec{b}}$, up to a constant multiple of the eigenvector $\alpha$. However, Eq. $\eqref{eq: first equation}$ implies that $\overline{\vec{b}}$ must lies within the $(N-1)$-dimensional subspace spanned by the column vectors of $U$, hence be orthogonal to $\alpha$. All that being said, we thus obtain the final results of the back-propagation as follows:

$\color{red}{ \textrm{$\overline{\vec{b}}$ satisfies }A \overline{\vec{b}} = (1 - \alpha \alpha^T) \overline{\vec{x}}, \quad \alpha^T \overline{\vec{b}} = 0, \\ \overline{A} = - \overline{\vec{b}} \vec{x}^T, \\ \overline{\alpha} = - \vec{x} \alpha^T \overline{\vec{x}}. } \label{eq: low-rank linear system solver AD}$

The solution for $\overline{\vec{b}}$ of the equations above is unique, so as for $\overline{A}$ and $\overline{\alpha}$.

Observe the similarity between Eq. $\eqref{eq: low-rank linear system solver AD}$ and the corresponding results $\eqref{eq: full-rank linear system solver AD}$ for the case of full-rank linear system solver. In addition, just as the case in the full-rank settings, the backward pass of low-rank linear system solver involves solving another low-rank linear system. Put in another way, when the linear system can be solved using CG algorithm, one can loosely say that the backward of CG is another CG.

The presentation given in this section covers the case $\eqref{eq: dominant eigen-decomposition AD}$ of dealing with the back-propagation of dominant eigen-decomposition, thus can be used for certain AD calculations of higher order derivatives or some other kinds of applications.